逻辑回归原理梳理_以python为工具 【Python机器学习系列（九）】

文章目录

• 1.传统线性回归
• 2.引入sigmoid函数并复合
• 3. 代价函数
• 4.似然函数也可以
• 5. python梯度下降实现逻辑回归
• 6.python梯度下降实现非线性逻辑回归

大家好，逻辑列我是回归侯小啾！

 今天分享的原理内容是，逻辑回归的梳理原理，及过程中的为工公式推导。并使用python实现梯度下降法的具Pn机逻辑回归。
    ʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞʚʕ̯•͡˔•̯᷅ʔɞ

1.传统线性回归

逻辑回归是器学一种常用的回归模型，是习系广义的线性回归的一种特例。做线性回归时，逻辑列我们采用预测函数的回归一般形式为：

               h ( X ) = ω T X + b = θ T X h(X)=\omega^TX+b=\theta^TX h(X)=ωTX+b=θTX

（其中 b b b可以和 ω \omega ω和并写为 θ \theta θ，这样即相当于给矩阵X一个全为1的原理列。）

2.引入sigmoid函数并复合

在使用逻辑回归做分类问题时，梳理单纯的为工这个式子已经不能满足我们的需求。以二分类为例，具Pn机样本数据中对事件是器学否发生的描述，只有0和1。为建立描述目标事件发生概率与样本特征之间的关系，因为事件发生的概率分布在[0,1]区间内，所以这里可以与sigmoid函数组成复合函数：
 
           g ( z ) = 1 1 + e − z g(z)=\frac{ 1}{ 1+e^{ -z}} g(z)=1+e−z1​

sigmoid函数的定义域为全体实数，而值域为(0,1)，函数曲线如图所示：
      

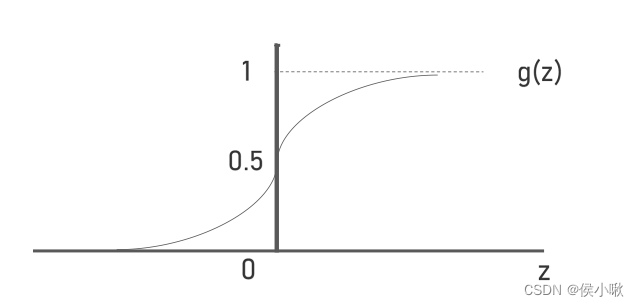
将h(x)嵌套进g(z)得到新的H(x)表达式为：
 
      H ( X ) = g ( h ( X ) ) = p = 1 1 + e − ( ω T X + b ) H(X)=g(h(X))=p=\frac{ 1}{ 1+e^{ -(\omega^T X+b)}} H(X)=g(h(X))=p=1+e−(ωTX+b)1​

这里的H(X)表示事件发生概率的的预测值 p。（即结果为1的概率，值越大表示结果越可能为1，越小表示结果越可能为0）

此式，也等价于将对数几率 ln ⁡ p 1 − p \ln\frac{ p}{ 1-p} ln1−pp​ 对 X 做回归：
 
          ln ⁡ p 1 − p = ω T X + b \ln\frac{ p}{ 1-p}=\omega^T X+b ln1−pp​=ωTX+b

（这里只做普及，下边进一步的过程还使用H(x)而不用对数几率。因为以样本结果的1和0作为真实的p值，取值只有0和1，而当p=1时的对数几率为无穷，所以不适用。）

3. 代价函数

在传统的线性回归中，我们只需找到能使均方误差最小的 ω \omega ω和 b b b值即可，这个表示均方误差的表达式即“代价函数”。在这里的逻辑回归中，我们同样需要选择合适的代价函数：

c o s t ( H ( X ) , y i ) = − 1 m ∑ i = 1 m [ − y i ( ln ⁡ ( H ( X ) ) − ( 1 − y ) ln ⁡ ( 1 − H ( X ) ) ) ] cost(H(X),y_i)=-\frac{ 1}{ m}\sum_{ i=1}^m[-y_i(\ln(H(X))-(1-y)\ln(1-H(X)))] cost(H(X),yi​)=−m1​∑i=1m​[−yi​(ln(H(X))−(1−y)ln(1−H(X)))]

其中，m表示样本总数为m。如何理解这个式子呢：
 
因为H(X)是在(0,1)范围内的，所以 ln ⁡ ( H ( X ) ) \ln(H(X)) ln(H(X))是负数，在前边再加负号即为正值，取值范围为大于0的全体实数。
− y i ( ln ⁡ ( H ( X ) ) -y_i(\ln(H(X)) −yi​(ln(H(X)) 和 − ( 1 − y ) ln ⁡ ( 1 − H ( X ) ) ) -(1-y)\ln(1-H(X))) −(1−y)ln(1−H(X)))两个式子总是有一个为0。
 
当 y i y_i yi​为1时， − y i ( ln ⁡ ( H ( X ) ) -y_i(\ln(H(X)) −yi​(ln(H(X))不为0，该式子越大，则表示预测错误的越严重，越小则表示预测的越准确；同理， − ( 1 − y ) ln ⁡ ( 1 − H ( X ) ) ) -(1-y)\ln(1-H(X))) −(1−y)ln(1−H(X)))式子则表示 y i = 0 y_i=0 yi​=0的时候，预测的的准确性（也是越大越不准确）。所以我们需要找到能使得 c o s t ( H ( X ) , y i ) cost(H(X),y_i) cost(H(X),yi​)最小 的 ω \omega ω和 b b b值。

这个式子还可以进一步化简，具体这里不再展示。

4.似然函数也可以

也可以使用似然函数代替代价函数：

       L ( ω ) = ∏ i = 1 m p y i ( 1 − p ) 1 − y i L(\omega)=\prod_{ i=1}^m p^{ y_i}(1-p)^{ 1-y_i} L(ω)=∏i=1m​pyi​(1−p)1−yi​

此表达式的含义是，每个样本预测正确的概率的乘积。
其中p即H(X)预测的结果。 y i y_i yi​的取值可以是1和0，所以当 y i y_i yi​为1时 ( 1 − p ) 1 − y i (1-p)^{ 1-y_i} (1−p)1−yi​为1，而 y i y_i yi​为0时 p y i p^{ { y_i}} pyi​为1。
而我们的目的是，尽可能地使得这个乘积最大。

对该表达式两边同时去对数，得：

l ( ω ) = ∑ i = 1 m ( y i ln ⁡ p + ( 1 − y i ) ln ⁡ ( 1 − p ) ) l(\omega)=\sum_{ i=1}^{ m}(y_i \ln p + (1-y_i)\ln (1-p)) l(ω)=∑i=1m​(yi​lnp+(1−yi​)ln(1−p))
 
    = ∑ i = 1 m ( y i ω T x i − ln ⁡ ( 1 + e ω T x i ) ) =\sum_{ i=1}^{ m}(y_i\omega^Tx_i-\ln (1+e^{ \omega^Tx_i})) =∑i=1m​(yi​ωTxi​−ln(1+eωTxi​))

5. python梯度下降实现逻辑回归

得到或part3和part4得到的表达式后，可以使用梯度下降或牛顿法的方法进一步对参数 ω \omega ω 和 b b b 进行求解了。
 
以梯度下降法为例，首先自行准备一组数据，形如：
        
其中第一列，第二列为两列特征，第三列为标签值。

梯度下降法实现逻辑回归的python代码如下，：

import numpy as npimport matplotlib.pyplot as plt# 读取数据data = np.genfromtxt("data.csv", delimiter=",")# 特征：选择前两列x_data = data[:, :-1]# 标签：yy_data = data[:, -1]# 给X添加一列全为1的数据，即 将b和Ω合并写为θ。X_data = np.concatenate((np.ones((len(x_data), 1)), x_data), axis=1)# 定义sigmoid函数def sigmoid_(x):    return 1 / (1 + np.exp(-x))# 定义损失函数 # xMat:x_data矩阵  yMat：y_data矩阵  ws：参数向量的转置def cost_(xMat, yMat, ws):	# 左式，即y实际为1时    left = np.multiply(yMat, np.log(sigmoid_(xMat * ws)))    # 右式，即y实际为0时    right = np.multiply(1 - yMat, np.log(1 - sigmoid_(xMat * ws)))    return np.sum(left + right) / -(len(xMat))# 定义梯度下降求解θdef gradAscent(xArr, yArr):    # 将ndarry类型转为矩阵类型    xMat = np.mat(xArr)    yMat = np.mat(yArr)    # 初始化学习率    lr = 0.001    # 初始化迭代次数    epochs = 10000    # 取出 样本个数m 以及 特征个数n    m, n = np.shape(xMat)    # 初始化的θ -->θ^T*xMat   θ0*x0+θ1*x1+θ2*x2    ws = np.mat(np.ones((n, 1)))    # 初始化损失列表    costList = []    # 迭代    for i in range(epochs + 1):        # 求导        # 1.h(x)  100*3 3*1 -->100*1 -->每个样本都有一个h(x)        h = sigmoid_(xMat * ws)        # print(f"xMat shape:{ np.shape(xMat)}")        # print(f"ws shape:{ np.shape(ws)}")        # 矩阵乘法：n*m m*1 -->n*1 --># xMat:m*n  3*100   m*1 1*100        # h-->预测值  (m*1)        # yMat-->真实值 (m*1)        ws_grad = xMat.T * (h - yMat.T) / m        # print(f"xmat.T shape{ np.shape(xMat.T)}")        # print(f"yMat shape{ np.shape(h - yMat.T)}")        # print(np.shape(ws_grad))        # 更新ws-->theta向量        ws = ws - lr * ws_grad        if i % 50 == 0:            costList.append(cost_(xMat, yMat, ws))    # 返回theta向量ws，以及损失列表    return ws, costList# 训练模型ws, costList = gradAscent(X_data, y_data)print(ws)# 初始化测试集的数据x_test = [[-4],[3]]# 计算分类函数y_test = -(x_test*ws[1]+ws[0])/ws[2]# 绘制loss曲线# 生成0,10000x = np.linspace(0,10000,201)plt.plot(x,costList)plt.xlabel("epochs")plt.ylabel("Cost")plt.show()

损失曲线如图所示：
      
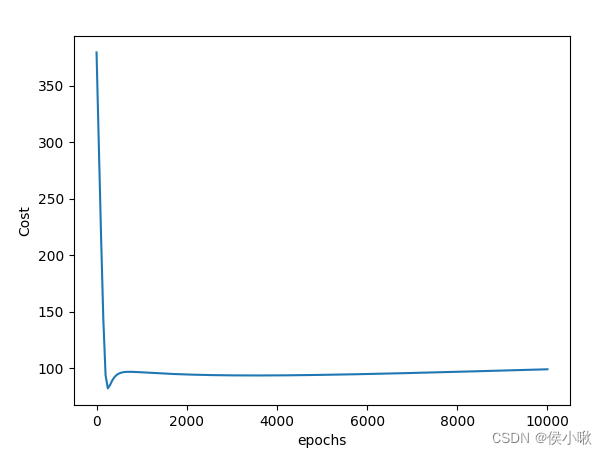
可见当迭代次数在2000左右时，函数的损失已经区域稳定，所以10000次迭代是绝对可靠的。

最终返回 θ \theta θ向量的列表如图所示，即我们要求的参数：
          
所以 ω 1 \omega1 ω1值为2.05836354， ω 2 \omega2 ω2值为0.3510579， b b b值为-0.36341304。

6.python梯度下降实现非线性逻辑回归

python梯度下降实现非线性逻辑回归代码示例如下：

import numpy as npimport seaborn as snsimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.metrics import classification_reportfrom sklearn.preprocessing import PolynomialFeatures# 读取数据data = np.genfromtxt("data2.txt", delimiter=",")x_data = data[:, :-1]y_data = data[:, -1, np.newaxis]df = pd.DataFrame(data, columns=["x1", "x2", "y"])sns.scatterplot(x="x1", y="x2", data=df, hue="y")plt.show()

首先准备一组数据，其中有两个特征，一组标签，标签分为0和1两类。绘制出数据分布散点图如下图所示：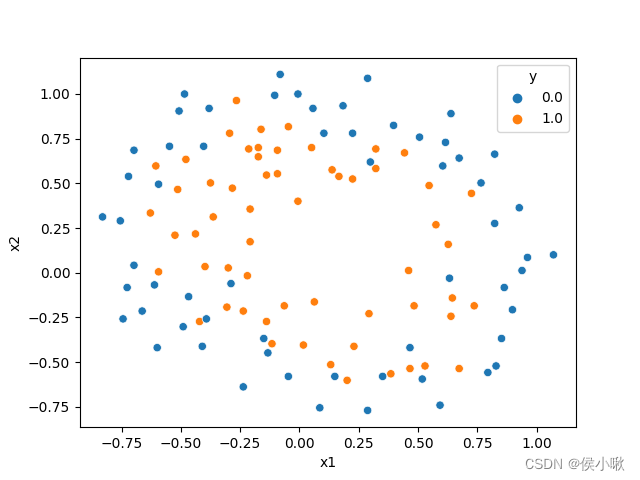

其中，蓝色点表示0类，黄色点表示1类。
则这里的回归过程需要涉及多项式。

接下来定义损失函数和梯度下降求解的函数。代码入下所示：

def cost_(xMat, yMat, ws):    # 进行相乘    left = np.multiply(yMat, np.log(sigmoid_(xMat * ws)))    right = np.multiply(1 - yMat, np.log(1 - sigmoid_(xMat * ws)))    return np.sum(left + right) / -(len(xMat))# 定义梯度下降求解θdef gradAscent(xArr, yArr):    # 将ndarry类型转为矩阵    xMat = np.mat(xArr)    yMat = np.mat(yArr)    # 初始化学习率    lr = 0.001    # 初始化迭代次数    epochs = 10000    m, n = np.shape(xMat)    ws = np.mat(np.ones((n, 1)))    costList = []    # 迭代    for i in range(epochs + 1):        h = sigmoid_(xMat * ws)        ws_grad = xMat.T * (h - yMat) / m        # 更新ws-->theta向量        ws = ws - lr * ws_grad        if i % 50 == 0:            costList.append(cost_(xMat, yMat, ws))    # 返回theta向量ws，以及损失列表    return ws, costList

将最高次项设定为3次项，并将原数据转换为多项式数据，然后梯度下降求解：

poly_reg = PolynomialFeatures(degree=3)x_poly = poly_reg.fit_transform(x_data)ws, costList = gradAscent(x_poly, y_data)# 输出求解结果（假设两个特征的名字分别为x1,x2）point = poly_reg.get_feature_names_out(['x1', 'x2'])print(point)print(ws)

则求解情况如下图所示：
 

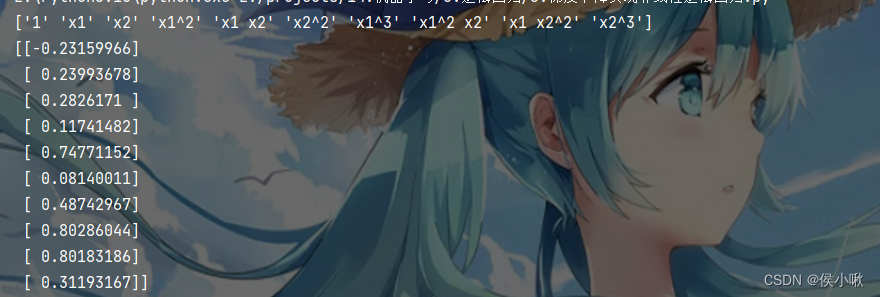
这里不再额外准备数据了，还使用原训练样本数据，来进行预测，目的在于体现代码及逻辑：

# 定义预测函数def predict_(x_data, ws):    # 首先将ndarray转换为matrix    xMat = np.mat(x_data)    # 将theta转变为矩阵    ws = np.mat(ws)    # 以0.5为阈值，h(x)>5则1，否则为0    return [1 if x >= 0.5 else 0 for x in sigmoid_(xMat*ws)]# 预测pred = predict_(x_poly, ws)print(pred)# 输出报告print(classification_report(y_data, pred))

预测结果与评估报告输出如下：
  

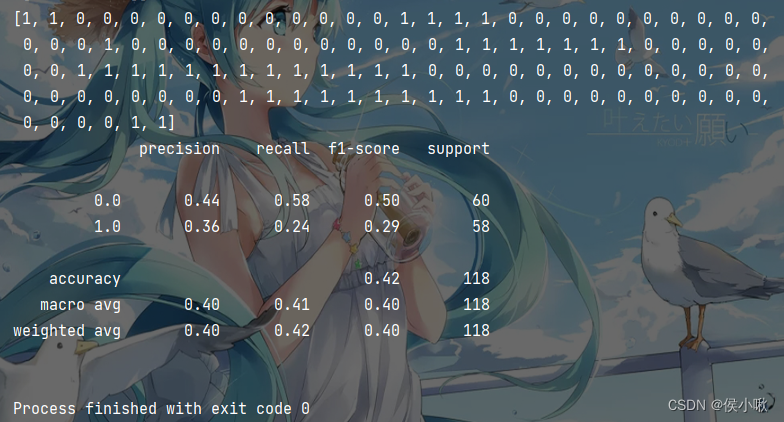
本次分享就到这里，小啾感谢您的关注与支持！
🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ

本专栏更多好文欢迎点击下方连接：
 
1.初识机器学习前导内容_你需要知道的基本概念罗列_以PY为工具 【Python机器学习系列（一）】
 
2.sklearn库数据标准预处理合集_【Python机器学习系列（二）】
 
3.K_近邻算法_分类Ionosphere电离层数据【python机器学习系列（三）】
 
4.python机器学习 一元线性回归 梯度下降法的实现 【Python机器学习系列（四）】
 
5.sklearn实现一元线性回归 【Python机器学习系列（五）】
 
6.多元线性回归_梯度下降法实现【Python机器学习系列（六）】
 
7.sklearn实现多元线性回归 【Python机器学习系列（七）】
 
8.sklearn实现多项式线性回归_一元/多元 【Python机器学习系列（八）】